Markov Transition Models
Time Series, Cross-Sectional Data
We are now entering the real world, as we will start to look at how characteristics vary, not only across different countries, but also across time. I have already presented the structure of time-series, cross-sectional (TSCS) data in Week 1, but to jog your memory, here it is again:

As you can see, each country has multiple observations, one for each year in which data have been observed. We will be using this information this week to calculate probabilities of regime transitions. For example, what is the probability of a country to transition from autocracy to democracy? As we only observe the regime type once for each year, this question alludes to the difference in regime type between two years in the same country. We will do this with a so-called Markov Transition Model.
What are Markov Transition Models?
A Markov Transition Model (MTM) models the probability of being a democracy in a particular year, given its regime type in the previous year. So, if we model the probability of a country to be a democracy this year, given that it was an autocracy in the previous year, we are modelling the probability of a transition from autocracy to democracy. Similarly, if we model the probability of a country to be a democracy this year, given that it was also a democracy in the previous year, we are modelling the probability of democratic survival. We can express these probabilities as so-called conditional probabilities.
Conditional Probabilities
Conditional probabilities express what I have described before in a formal way. The conditional probability to model for democratic emergence is written as follows:
\[\begin{equation} P(y_{i,t} = 1 | y_{i, t-1} = 0) \end{equation}\]
This reads: The probability of a country i to be a democracy (y=1) in year t, given (this is what the vertical line | says) that country i was an autocracy (y=0) in the previous year (t-1). Analogously, the conditional probability for democratic survival is:
\[\begin{equation} P(y_{i,t} = 1 | y_{i, t-1} = 1) \end{equation}\]
This reads: The probability of a country i to be a democracy (y=1) in year t, given that country i was also a democracy (y=1) in the previous year (t-1).
We will now apply this knowledge to create a model in R which calculates these conditional probabilities. Let’s start with democratic emergence.
Democratic Emergence
Democratic emergence is expressed as the probability of a country to be a democracy in year \(t\), given that it was a dictatorship in the previous year, \(t-1\)
\[\begin{equation*} P(y_{i,t} = 1 | y_{i, t-1} = 0) \end{equation*}\]
As a first step, we therefore need a variable that gives us the information which regime type each of our countries had in the previous year. We will use the world data set for this illustration.
We can now create the lagged democracy value. In order for R to know when a new country “starts”, we need to group observations by country first, and then lag the variable democracy. We do this with the intuitively called function lag(). We then ungroup the data again, as we have no need of the groups any more.
This creates a new variable l.democracy which gives us the information we were after: the regime type of the country in the previous year. Note that as the first observation for each country cannot be lagged, it creates as many missing values as we have countries in the data set. Perhaps this makes more sense with a visualisation:
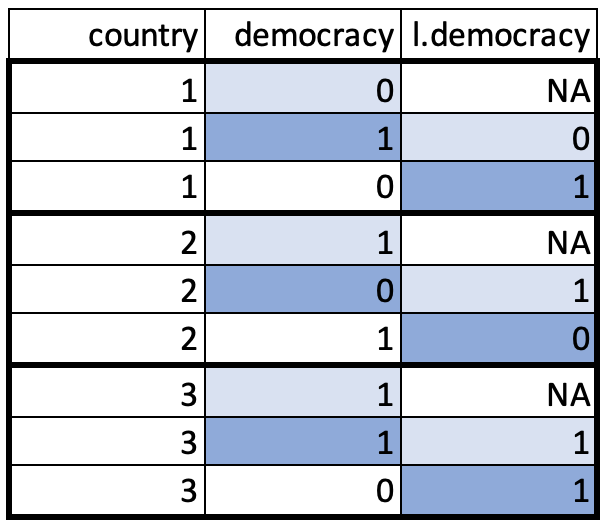
Lagging the Independent Variables
So far, we have lagged the dependent variable, to run an MTM. This was a methodological necessity. But from a substantive point of view it makes sense to also lag our independent variables. It is reasonable to assume, that the regime type in year \(t\) depends on the state of socio-economic development in the previous year, \(t-1\). It is rare that for example a recession hits, and the country immediately changes regime type. These things need time. And this is why we will now also lag the independent variables.
This is the same procedure as before. For “per capita GDP” we call:
Let’s do the same for life expectancy:
and Primary gross enrolment rate:
Subsetting the Data for Conditional Probabilities
Recall that for democratic emergence we need all of those observations in which a country has been an autocracy in the previous year. We can select these in R by filtering the data:
Whilst we are at it, we might as well also do this for democratic survival. Here we need all observations in which l.democracy=1
And with that we are ready!
Democratic Emergence
Even though “Markov Transition Model” sounds very complicated, the code in R is actually no different from a “regular” probit model. The only difference is that we have selected a certain type of observations. For emergence we call:
emergence <- glm(democracy ~ l.gdppc,
data = world_democ0,
na.action = na.exclude,
family = binomial(link = "probit"))
summary(emergence)
Call:
glm(formula = democracy ~ l.gdppc, family = binomial(link = "probit"),
data = world_democ0, na.action = na.exclude)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.967e+00 5.170e-02 -38.052 <2e-16 ***
l.gdppc -3.201e-05 1.558e-05 -2.054 0.04 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 794.78 on 3879 degrees of freedom
Residual deviance: 787.79 on 3878 degrees of freedom
(1099 observations deleted due to missingness)
AIC: 791.79
Number of Fisher Scoring iterations: 8Once again, we can include multiple independent variables by connecting these with + in the glm() function:
emergence_full <- glm(democracy ~ l.gdppc + l.life +
l.enrol_gross,
data = world_democ0,
na.action = na.exclude,
family = binomial(link = "probit"))
summary(emergence_full)
Call:
glm(formula = democracy ~ l.gdppc + l.life + l.enrol_gross, family = binomial(link = "probit"),
data = world_democ0, na.action = na.exclude)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.706e+00 3.683e-01 -7.346 2.05e-13 ***
l.gdppc -7.424e-05 2.906e-05 -2.554 0.0106 *
l.life 1.810e-02 7.848e-03 2.306 0.0211 *
l.enrol_gross -2.358e-03 2.510e-03 -0.939 0.3476
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 664.33 on 2845 degrees of freedom
Residual deviance: 650.69 on 2842 degrees of freedom
(2133 observations deleted due to missingness)
AIC: 658.69
Number of Fisher Scoring iterations: 9Democratic Survival
Modelling democratic survival is easy now, as we have already completed all necessary preparations. To model
\[\begin{equation*} P(y_{i,t} = 1 | y_{i, t-1} = 1) \end{equation*}\]
we call:
survival <- glm(democracy ~ l.gdppc,
data = world_democ1,
na.action = na.exclude,
family = binomial(link = "probit"))
summary(survival)
Call:
glm(formula = democracy ~ l.gdppc, family = binomial(link = "probit"),
data = world_democ1, na.action = na.exclude)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.627e+00 8.555e-02 19.019 < 2e-16 ***
l.gdppc 2.268e-04 4.788e-05 4.738 2.16e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 583.28 on 3791 degrees of freedom
Residual deviance: 503.78 on 3790 degrees of freedom
(385 observations deleted due to missingness)
AIC: 507.78
Number of Fisher Scoring iterations: 11And again with all independent variables:
survival_full <- glm(democracy ~ l.gdppc + l.life +
l.enrol_gross,
data = world_democ1,
na.action = na.exclude,
family = binomial(link = "probit"))
summary(survival_full)
Call:
glm(formula = democracy ~ l.gdppc + l.life + l.enrol_gross, family = binomial(link = "probit"),
data = world_democ1, na.action = na.exclude)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 8.398e-01 6.069e-01 1.384 0.16645
l.gdppc 1.373e-04 4.842e-05 2.836 0.00457 **
l.life 7.953e-03 1.182e-02 0.673 0.50122
l.enrol_gross 4.130e-03 3.675e-03 1.124 0.26105
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 414.00 on 2915 degrees of freedom
Residual deviance: 357.24 on 2912 degrees of freedom
(1261 observations deleted due to missingness)
AIC: 365.24
Number of Fisher Scoring iterations: 11