Worksheet Week 1

Self-Assessment Questions¹

What do cross-tabulations do?
Can we use continuous variables for cross-tabulations?
What are the strengths and weaknesses of cross-tabulations?
Why do we calculate the $\chi^2$ -value as $\chi^{2} = \Sigma \frac{(f_{o}-f_{e})^{2}}{f_{e}}$ ?
How does the $\chi^2$ distribution differ from the t- and normal distribution?

Please stop here and don’t go beyond this point until we have compared notes on your answers.

Calculations by Hand

I have given you an example of a cross-tabulation in the lecture. Consider the following Table:

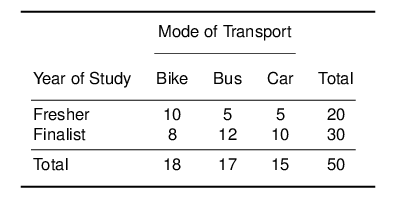
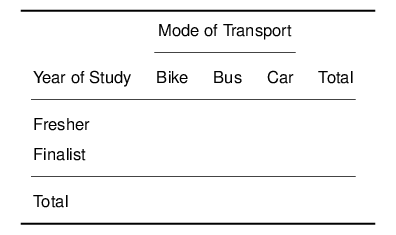
Calculate the Expected Values and fill in the following table:

Calculate the $\chi^{2}$ -value
How many degrees of freedom does this table have? Why?
Using the $\chi^2$ Table, what is the p-value?
Are mode of transport and year of study independent in the population?

Cross-Tabulations in R

If you have joined PO12Q without suffering through PO11Q, then please work through Weeks 5 and 7 of PO11Q before proceeding with the present material:

Data Set

We are working with the World Development Indicators this week. Data are taken from World Bank (2024), Boix et al. (2018), and Marshall & Gurr (2020). For more information on the democracy coding by Boix et al. please download and read the corresponding paper.
Download the data WDI_PO12Q.csv and place it in a new working directory for this week
The variables we will be working with today are as follows:

Table 1: WDI Codebook
variable	label
Country Name	Country Name
Country Code	Country Code
year	year
democracy	0 = Autocracy, 1 = Dictatorship (Boix et al., 2018)
gdppc	GDP per capita (constant 2010 US$)
gdpgrowth	Absolute growth of per capita GDP to previous year (constant 2010 US Dollars)
enrl_gross	School enrollment, primary (% gross)
enrl_net	School enrollment, primary (% net)
agri	Employment in agriculture (% of total employment) (modeled ILO estimate)
slums	Population living in slums (% of urban population)
telephone	Fixed telephone subscriptions (per 100 people)
internet	Individuals using the Internet (% of population)
tax	Tax revenue (% of GDP)
electricity	Access to electricity (% of population)
mobile	Mobile cellular subscriptions (per 100 people)
service	Services, value added (% of GDP)
oil	Oil rents (% of GDP)
natural	Total natural resources rents (% of GDP)
literacy	Literacy rate, adult total (% of people ages 15 and above)
prim_compl	Primary completion rate, total (% of relevant age group)
infant	Mortality rate, infant (per 1,000 live births)
hosp	Hospital beds (per 1,000 people)
tub	Incidence of tuberculosis (per 100,000 people)
health_ex	Current health expenditure (% of GDP)
ineq	Income share held by lowest 10%
unemploy	Unemployment, total (% of total labor force) (modeled ILO estimate)
lifeexp	Life expectancy at birth, total (years)
urban	Urban population (% of total population)
polity5	Combined Polity V score

Loading the Data

setwd("~/PO12Q/Seminars/PO12Q_Seminar_Week 1")
wdi <- read.csv("WDI_PO12Q.csv")

You can copy the code from this page by hovering over the code chunk and clicking the icon in the top-right hand corner. You can then paste it into your RScript.

Guided Example

We are now going to use the WDI, and produce a crosstab of life expectancy at birth, total (years) by GDP per capita (constant 2010 US$), using the variables lifeexp and gdppc
We first need to recode both variables into factor variables, as these are continuous.
First up is lifeexp
Recoding: as a refresher from PO11Q, we are specifying the new data frame as the old one, then we add a pipe, and call the function mutate. Therein, we create a new variable called lifecat, which will be an ordered factor, cutting the variable life at the stated intervals, and labeling these levels accordingly.

library(tidyverse)

wdi <- wdi %>% 
  mutate(lifecat=
           ordered(
             cut(lifeexp, breaks=c(0,77,84), 
                 labels=c("low","high"))))

Make a habit of adding a note underneath each code chunk in your RScript (with a ‘#’) in which you translate the code into plain English.

Next up is gdppc which we are recoding into a factor variable with three levels:

wdi <- wdi %>% 
  mutate(gdpcat=
           ordered(
             cut(gdppc, breaks=c(0,3861.5,25260, 150000), 
                 labels=c("low","medium", "high"))))

Let us now see whether the level of GDP has an influence on life expectancy
State the null and the alternative hypothesis (directional)
Run the cross-tabulation, by calling:

wdi_table <- with(wdi, table(gdpcat, lifecat))
wdi_table
        lifecat
gdpcat   low high
  low     69    0
  medium  54   16
  high     3   27

Now perform a chi-squared test, using the command²

Xsq <- chisq.test(wdi_table, correct=FALSE)
Xsq

    Pearson's Chi-squared test

data:  wdi_table
X-squared = 89.702, df = 2, p-value < 2.2e-16

As on PO11Q, I have prepared flashcards to help you learn R functions. These have their own section each week in this companion, but are also available on the more general POQ Flashcard Page.

Are the results statistically significant? At what level?
What do these results mean for our hypotheses?
Produce the table of expected frequencies, using the command

round(Xsq$expected, 2)
        lifecat
gdpcat     low  high
  low    51.44 17.56
  medium 52.19 17.81
  high   22.37  7.63

You can compare that to the observed ones:

round(Xsq$observed, 2)
        lifecat
gdpcat   low high
  low     69    0
  medium  54   16
  high     3   27

You can see that this is identical to producing the cross-tabulation in the first place:

wdi_table
        lifecat
gdpcat   low high
  low     69    0
  medium  54   16
  high     3   27

In plain English: What have we found out?

Exercises

Let us find out whether the completion of primary school influences unemployment rates.
1. State the null and directional alternative hypothesis for this test.
2. Create a new variable primary_fac using the prim_compl variable. Cut it into three categories “low”, “medium”, and “high”, cutting prim_compl at its first quartile, and its mean.
3. Apply the same procedure to unemploy, creating a new variable called unemp_fac.
4. Create a cross-tabulation assessing the dependence of unemployment on primary completion rate. unemp_fac.
5. Test whether the dependence is statistically significant. unemp_fac.
Repeat steps 1a) to 1e) for two variables of your own choice.

Homework for Week 2

Read the items marked “essential” on the reading list (see Talis)
Work through this and next week’s “Methods, Methods, Methods” Sections.
Work through this week’s flashcards to familiarise yourself with the relevant R functions.
Find an example for each NEW function and apply it in R to ensure it works
Complete the Week 1 Moodle Quiz

Solutions

You can find the Solutions in the Downloads Section.

Some of the content of this worksheet is taken from Reiche (forthcoming).↩︎
I am using the correct=FALSE option here to reproduce the $\chi^{2}$ -value you would get if you calculated this by hand. Technically, $\chi^{2}$ is only an approximation of the hypergeometric distribution which would deliver an exact test. You can get the precise value by applying Yates’ continuity correction with correct=TRUE.↩︎