Additional Exercises

Load Packages and data11

Before starting, we need to load libraries and install packages if not already installed. In these exercises we will be using the following packages:

  1. haven
  2. ggplot2
  3. stargazer

Set working directory and load the data file simd.csv into R. This is the “Scottish Index of Multiple Deprivation”. Here is the codebook:

Table 6: Codebook for simd Data Set
Variable Label
Data_Zone 2011 Data Zone
Intermediate_Zone 2011 Intermediate Zone name
Council_area Council area name
Total_population 2017 NRS small area population estimates
Working_age_population 2017 NRS small area population estimates and state pension age
Income_rate Percentage of people who are income deprived
Income_count Number of people who are income deprived
Employment_rate Percentage of people who are employment deprived
Employment_count Number of people who are employment deprived
CIF Comparative Illness Factor: standardised ratio
ALCOHOL Hospital stays related to alcohol use: standardised ratio
DRUG Hospital stays related to drug use: standardised ratio
mortality Standardised mortality ratio
DEPRESS Proportion of population being prescribed drugs for anxiety, depression or psychosis
LBWT Proportion of live singleton births of low birth weight
EMERG Emergency stays in hospital: standardised ratio
Attendance School pupil attendance
Attainment Attainment of school leavers
no_qualifications Working age people with no qualifications: standardised ratio
not_participating Proportion of people aged 16-19 not participating in education, employment or training
University Proportion of 17-21 year olds entering university
drive_petrol Average drive time to a petrol station in minutes
drive_GP Average drive time to a GP surgery in minutes
drive_PO Average drive time to a post office in minutes
drive_primary Average drive time to a primary school in minutes
drive_retail Average drive time to a retail centre in minutes
drive_secondary Average drive time to a secondary school in minutes
PT_GP Public transport travel time to a GP surgery in minutes
PT_Post Public transport travel time to a post office in minutes
PT_retail Public transport travel time to a retail centre in minutes
broadband Percentage of premises without access to superfast broadband (at least 30Mb/s download speed)
crime_count Number of recorded crimes of violence, sexual offences, domestic housebreaking, vandalism, drugs offences, and common assault
crime_rate Recorded crimes of violence, sexual offences, domestic housebreaking, vandalism, drugs offences, and common assault per 10,000 people
overcrowded_count Number of people in households that are overcrowded
nocentralheat_count Number of people in households without central heating
overcrowded_rate Percentage of people in households that are overcrowded
nocentralheat_rate Percentage of people in households without central heating
sim_rank Rank of data zones from most deprived (ranked 1) to least deprived (ranked 6,976)

Inspect your data

Here you can use several basic functions. The dataset does not contain too many variables, so you can start by using names(), str(), dim(), etc.

The function dim() is new. What does it do?

Preliminary Analysis

Now that you have a preliminary idea of the structure of the dataset, you can select two variables and test a possible relationship. The topic today is bivariate linear regression analysis, so remember that the outcome variable needs to be continuous.

Let’s say we want to look at the relationship between alcohol consumption and mortality rate (yes, not a very funny topic, but interesting nonetheless). The two variables are, respectively, ALCOHOL and SMR.

Now, formulate the working (alternative) and the null hypothesis.

H\(\pmb{_0}\):

H\(\pmb{_1}\):

Which is your dependent variable?

Run a frequency table on the mortality variable. What is the level of measurement?

Do the same for the other variable. And guess what is the level of measurement.

Visualisation

Let’s start with the visualisation of the relationship between the two variables. Use a scatterplot to visualise the relationship and add the regression line.

You can use ggplot, but also the standard plot() function.

Improve the initial graph by:

  1. Adding a regression line.
  2. Adding up a relevant title, also possibly a subtitle.
  3. Adding axes labels and making them readable.
  4. Remove the grid in the background.

The result should be Figure 1.

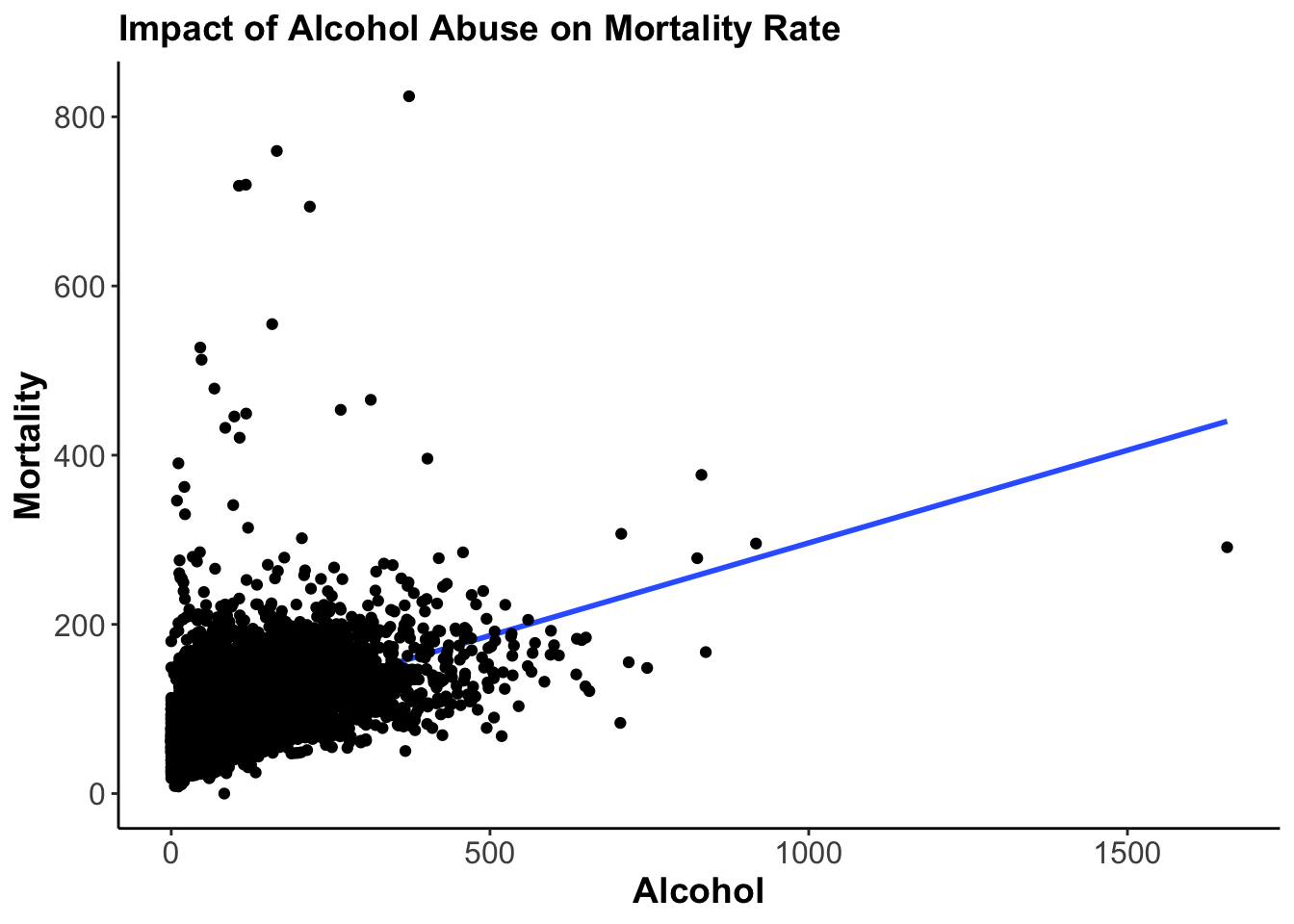
\label{fig:alcsmr}Improved Graph

Figure 1: Improved Graph

If you have done everything correctly, you should see that the dots are rather concentrated in the bottom left corner of the scatterplot with some outliers far away from the cloud of our data. It is not a big deal, but we might want to get rid of the outliers and this way improve our visualisation.

There are several ways to do that, of course. But let’s say we want to transform our variables, excluding all values over a certain point. For instance, we want to exclude the values above 750 of our alcohol variable and above 500 for our mortality variable. How would you do that?

There are – of course – several solutions. One could be, to create a new datset, subsetting the original. Another solution could be to create a new variable telling R to transform all the values above our treshold in NA. Try to find an apply the appropriate code. Use Google if necessary, it helps a lot.

Visualisation 2.0

Now, visualise the relationship using the reduced data frame. What can you see?

You can improve the scatterplot using a series of arguments (e.g., alpha) in the geom_point() function in ggplot. Try to improve the Aesthetics of the scatterplot playing with alpha, for instance. (see R Documentation).

Also, you can draw a vertical and horizontal line corresponding to the mean of your variables using geom_hline and geom_vline. You can thus check if the regression line passes through the mean of X and Y. (see R Documentation).

Remember that Google is your best friend when you learn to code. And after that as well. No one actually remembers all the functions and all their argument. The secret is to know how to google the things you need.

Saving the Scatterplot

You can also save a graph as .png, .JPG (even .pdf) that you can then import in a word document. Although there are many way to use your R output, saving a graph might be sometimes useful.

Use the function ggsave() to save your scatterplot. Again, there are tons of examples online, google it.

You first need to store the graph in an object.

Regression Analysis (yes, finally)

Now we can finally run a linear regression with mortality as the outcome variable and alcohol as the predictor using the lm() function. Store the results in an object called model and visualise the regression output using summary(). Use the reduced data set without outliers.


Call:
lm(formula = SMR ~ ALCOHOL, data = simred)

Residuals:
    Min      1Q  Median      3Q     Max 
-146.54  -22.63   -4.72   16.73  387.27 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 76.733653   0.636021  120.65   <2e-16 ***
ALCOHOL      0.217635   0.004579   47.53   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 36.13 on 6959 degrees of freedom
Multiple R-squared:  0.2451,    Adjusted R-squared:  0.2449 
F-statistic:  2259 on 1 and 6959 DF,  p-value: < 2.2e-16

You can also extract specific blocks of the output table. One way of doing it is to use the brackets [] after the summary() function. For example summary()[8]. Try to extract the block of Coefficients from the table, like this:

$coefficients
              Estimate  Std. Error  t value Pr(>|t|)
(Intercept) 76.7336534 0.636021422 120.6463        0
ALCOHOL      0.2176351 0.004579103  47.5279        0

As you go through the different numbers, take note which component of the regression output is associated with which number.

Interpretation

Interpret the results, starting with model evaluation.

  1. How much variation in the outcome variable does the model explain? What does this tell us about the model?
  2. Interpret the slope coefficient.
  3. Interpret the intercept? What does it mean in practice?
  4. Interpret the results (in plain language) referring to the hypothesis you formulated above.

Exporting the Results

Just as with graphs, you can also export and save the results of the regression model in a Word table. To do that you can use the stargazer package. Try and export the table.

The stargazer function needs to contain, in order: the name of the R object where you stored the regression results, the option header=F to suppress the annoying immortalisation of the author, the option type="html", and the option out="documentname.doc" which places a word document with that file name in your working directory.

Should you use MS Word to write your essay and your essay is saved in your working directory, do not save the table document under the same name as your essay, as R will overwrite it and it will be gone forever.

You can improve the table in many ways. For example, you need to replace the variable names with the variable labels. You could also add a name of the model, and suppress unneeded statistics.

If you have done everything correctly, you should receive something similar to this:

   
Table 7: Impact of Alcohol Abuse on Mortality in Scotland
Dependent variable:
Standardised Mortality Ratio
Hospital Stays related to Alcohol Use 0.218***
(0.005)
Constant 76.734***
(0.636)
Observations 6,961
R2 0.245
Note: *p<0.1; **p<0.05; ***p<0.01

   

Comparing models

You can now run another regression model with a different independent variable. Can you compare your original model with the new one? How? How do you know which independent variable is doing a better job in explaining your dependent variable?

Homework for Week 8

Solutions

You can find the Solutions in the Downloads Section.

  1. These exercises were originally written by Oleksiy Bondarenko who taught the module in 2022/23. I have slightly altered them in subsequent years.↩︎