Worksheet Week 3

Self-Assessment Questions⁷

1. Explain the difference between $\hat{y}_i$ and $y_i$.
2. Give an example for a scenario in which you could use regression analysis.
3. Why is there an error term in regression?
4. How does an error term differ from a residual?
5. Explain what the conditional expectation function (CDF) means in plain English.

Please stop here and don’t go beyond this point until we have compared notes on your answers.

---

Regression – Theory

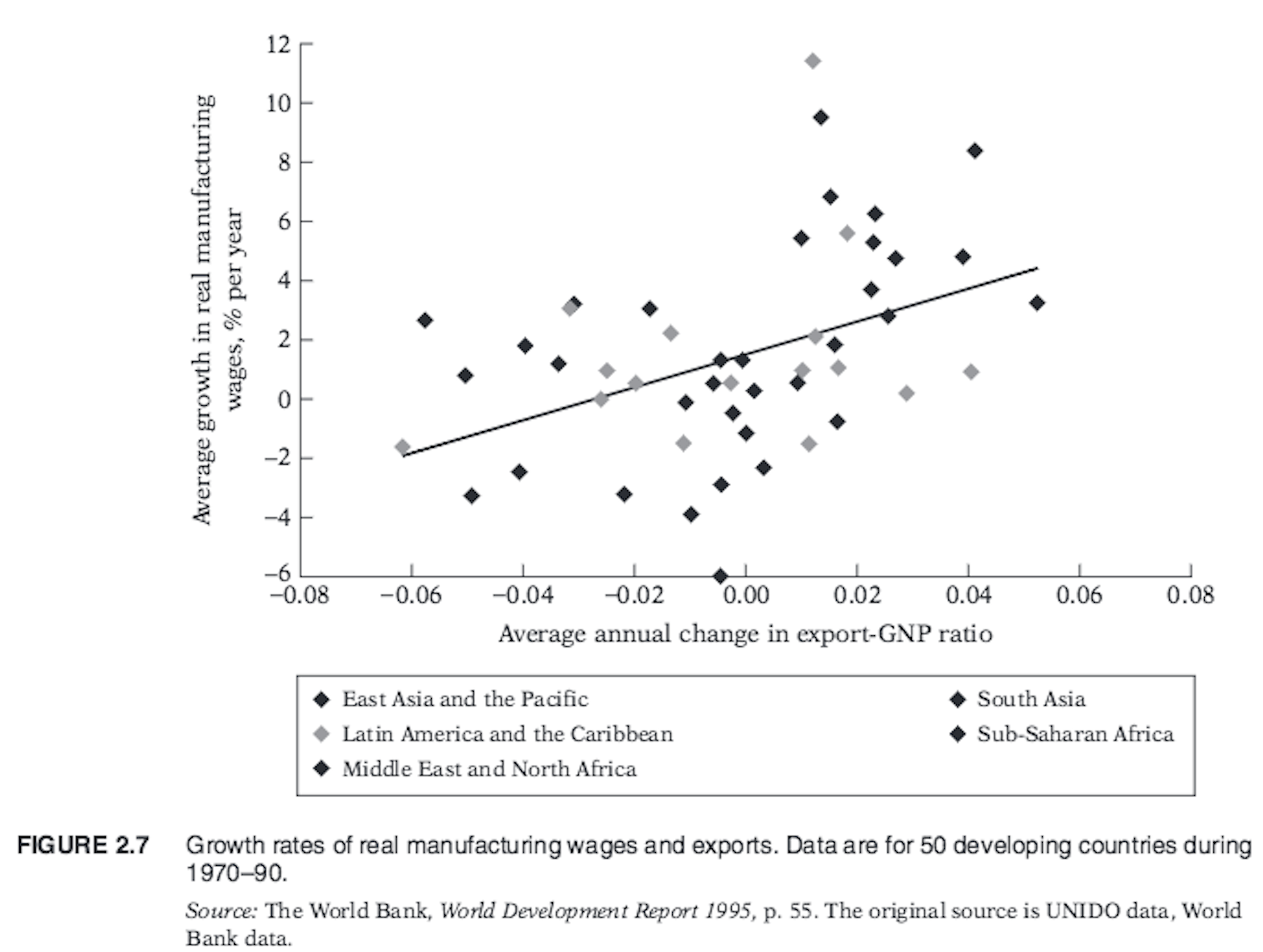
1. You are given the scatter plot in Figure 2.7 (taken from Gujarati & Porter, 2009, p. 50) along with the regression line. What general conclusion do you draw from this diagram? Is the regression line sketched in the diagram a population regression line or a sample regression line?

---

Calculations with Matrices

We will start working with matrices next week. To familiarise yourself with these and to get a better overview how to work with them, please work through the following exercises. Feel free to consult the “Introduction to Matrices” Section for this.

First, answer these questions:

• What is a matrix?
• What does transposition do?
• What is the purpose of an identity matrix?

Now, consider the following three matrices A, B, and C: $$\begin{equation*} A = \begin{bmatrix} 9 & 4 & 11 \\ 6 & 8 & 3 \\ 14 & 7 & 9 \\ \end{bmatrix} \hspace{1cm} B = \begin{bmatrix} 13 & 8 & 12 & 2 \\ 1 & 5 & 15 & 3 \\ \end{bmatrix} \hspace{1cm} C = \begin{bmatrix} 25 & 22 \\ 31 & 19 \\ \end{bmatrix} \end{equation*}$$

1. What is the value in:

   1. $A_{22}$
   2. $A_{31}$
   3. $B_{13}$
   4. $B_{24}$
   5. $C_{12}$
   6. $C_{21}$

2. Transpose $B$ into $B^\prime$ using the following blank matrix. $$\begin{equation*} B^\prime = \begin{bmatrix} & & & &\\ & & & &\\ & & & &\\ & & & &\\ \end{bmatrix} \end{equation*}$$

3. Solve $D$ where $C \times B = D$ using the following blank matrix. $$\begin{equation*} D = \begin{bmatrix} & & & & & &\\ & & & & & &\\ & & & & & &\\ & & & & & &\\ \end{bmatrix} \end{equation*}$$

4. Solve $C^{-1}$, showing your workings using the appropriate formula. $$\begin{equation*} C^{-1} = \frac{\:}{\hspace{2.5cm}} \begin{bmatrix} & & & & \\ & & & & \\ \end{bmatrix} \hspace{2.5mm}=\hspace{2.5mm} \begin{bmatrix} & & & & \\ & & & & \\ \end{bmatrix} \end{equation*}$$

---

Homework for Week 4

• There is no separate reading for the seminar in Week 4
• Work through the Week 4 “Methods, Methods, Methods” Section.
• Work through this week’s flashcards to familiarise yourself with the relevant R functions.
• Find an example for each NEW function and apply it in R to ensure it works
• Complete the Week 3 Moodle Quiz
• Familiarise yourself further with matrices by setting yourself two sample matrices, A and B (each should be a 2x2 matrix). Conduct the following operations:
  • Multiply A and B
  • Invert A and B
  • Transpose A and B
  • Multiply A with an Identity Matrix
  • Multiply A with A$^{-1}$. What is the result called?

You can check your solutions with https://matrixcalc.org/ . You can also try to figure out how to do this in R. This is a great way to practice working with matrices until you are familiar with the procedure.

---

---

7. Some of the content of this worksheet is taken from Reiche (forthcoming).↩︎