z-Scores

Self-Assessment Questions9

  1. How do the probability distributions of a discrete and a continuous variable differ?
  2. What is a sample distribution?
  3. How does the sample distribution differ from the sampling distribution?
  4. Why do we need the sampling distribution?
  5. What is the difference between the standard deviation and the standard error?

Please stop here and don’t go beyond this point until we have compared notes on your answers.

How to read a z-table

In the lecture you have learned about the Normal Distribution. Under the Normal Distribution, the area under the curve is determined by the number of standard deviations around our mean \(\mu\). This number is expressed in the form of the z-score which is defined as:

\[\begin{equation} z=\frac{\text{Observation} - \text{Mean}}{\text{Standard Deviation}}=\frac{y-\mu}{\sigma} \end{equation}\]

To put this in words, z takes the difference between a particular value we are interested in and the mean. It then divides this distance by the standard deviation, in order to express the distance in units of standard deviations. Why do we do this? We know that under the Normal Distribution the area of the interval mean \(\pm\) one standard deviation is equal to 68%. This is equivalent to the blue area in Figure 5. This also means that the remaining white area is equal to 32%, or the white section on each side 16%.

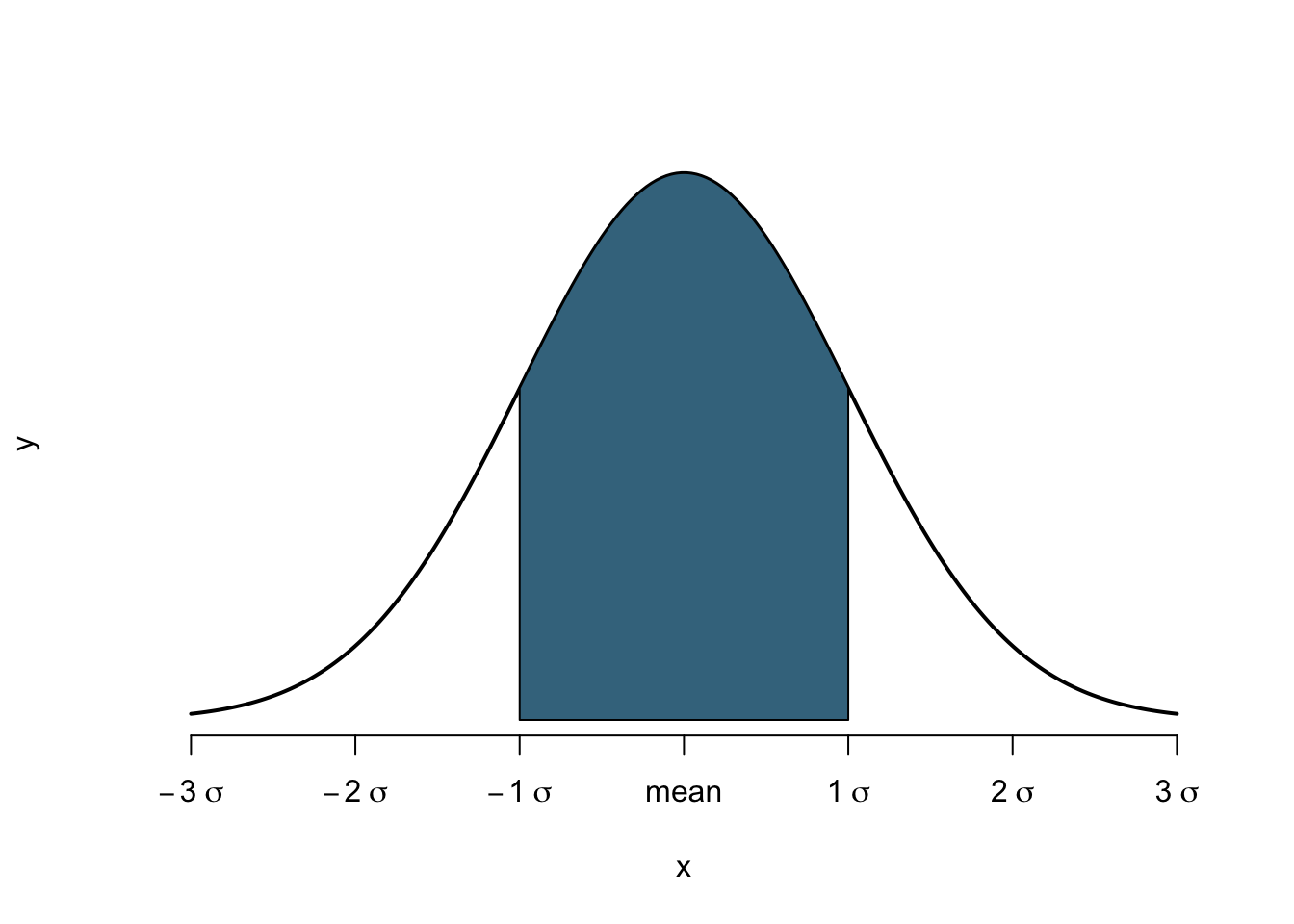
\label{fig:area68}Area under the Normal Distribution

Figure 5: Area under the Normal Distribution

Imagine now, we took the point of minus one standard deviation as a starting point, and turn right, as in Figure 6. The white area is still 16%, so that the blue area needs to be 84%.

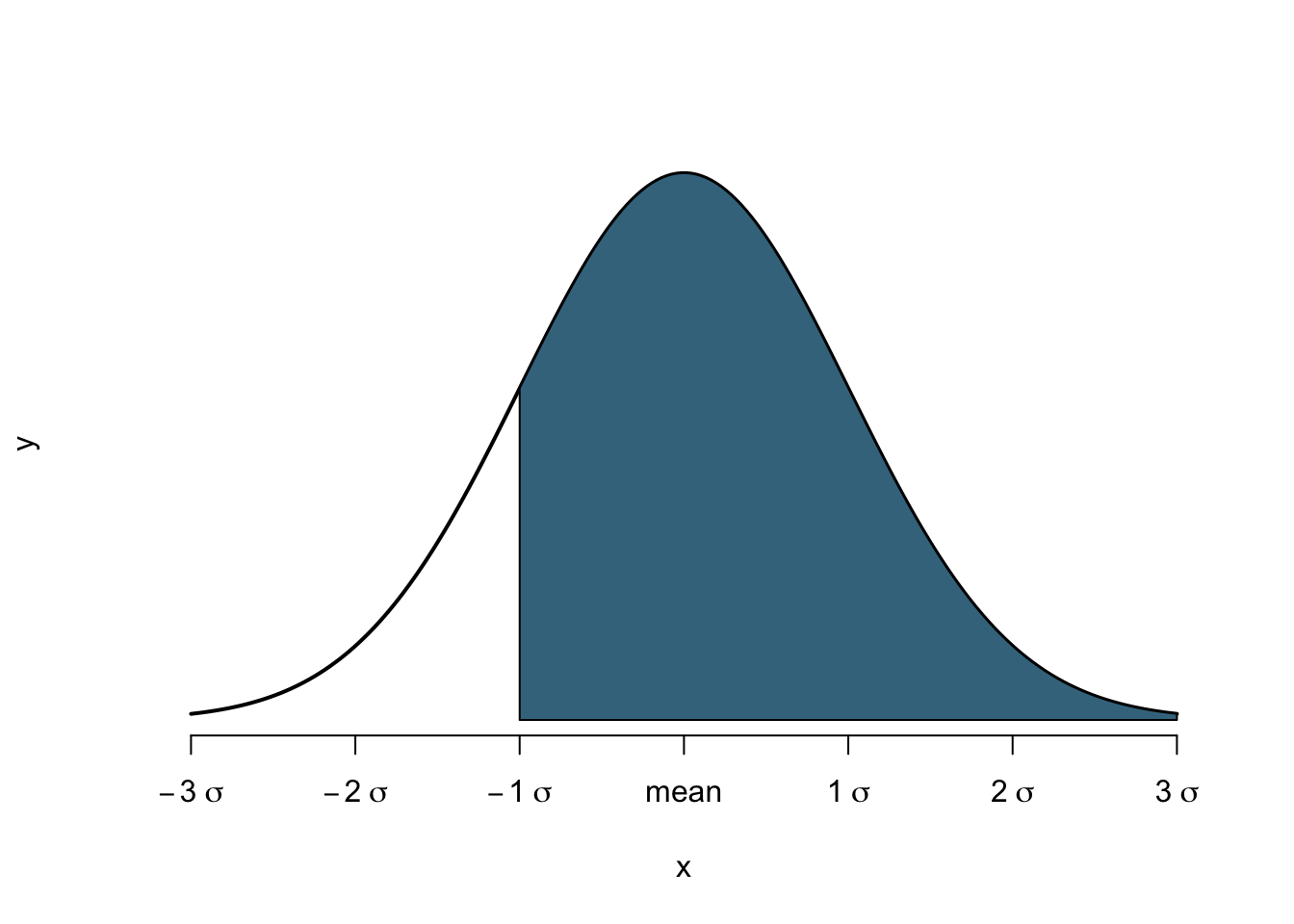
\label{fig:area84}Right-Tail Probability

Figure 6: Right-Tail Probability

So the probability of finding a value larger than what is equivalent to minus one standard deviation is 84%. We call this a right-tail probability. The beauty is that we can do this for any point on the x-axis. Once we know how many standard deviations a value is removed from the mean, we can use the right-tail probability to assess how likely a value higher (or lower) than this value is to occur.

The number of standard deviations is the z-score. Every z-score has a right-tail probability associated with it. These probabilities are listed in the Normal Table (see Moodle). How do we read this Table? Let me take you through the example used in the lecture once more. We assumed that the voter turnout rates of the 2019 European Elections for 28 countries was normally distributed, with \(\mu=50.66\) and \(\sigma=16.56\). You can see this distribution visualised in Figure 7.

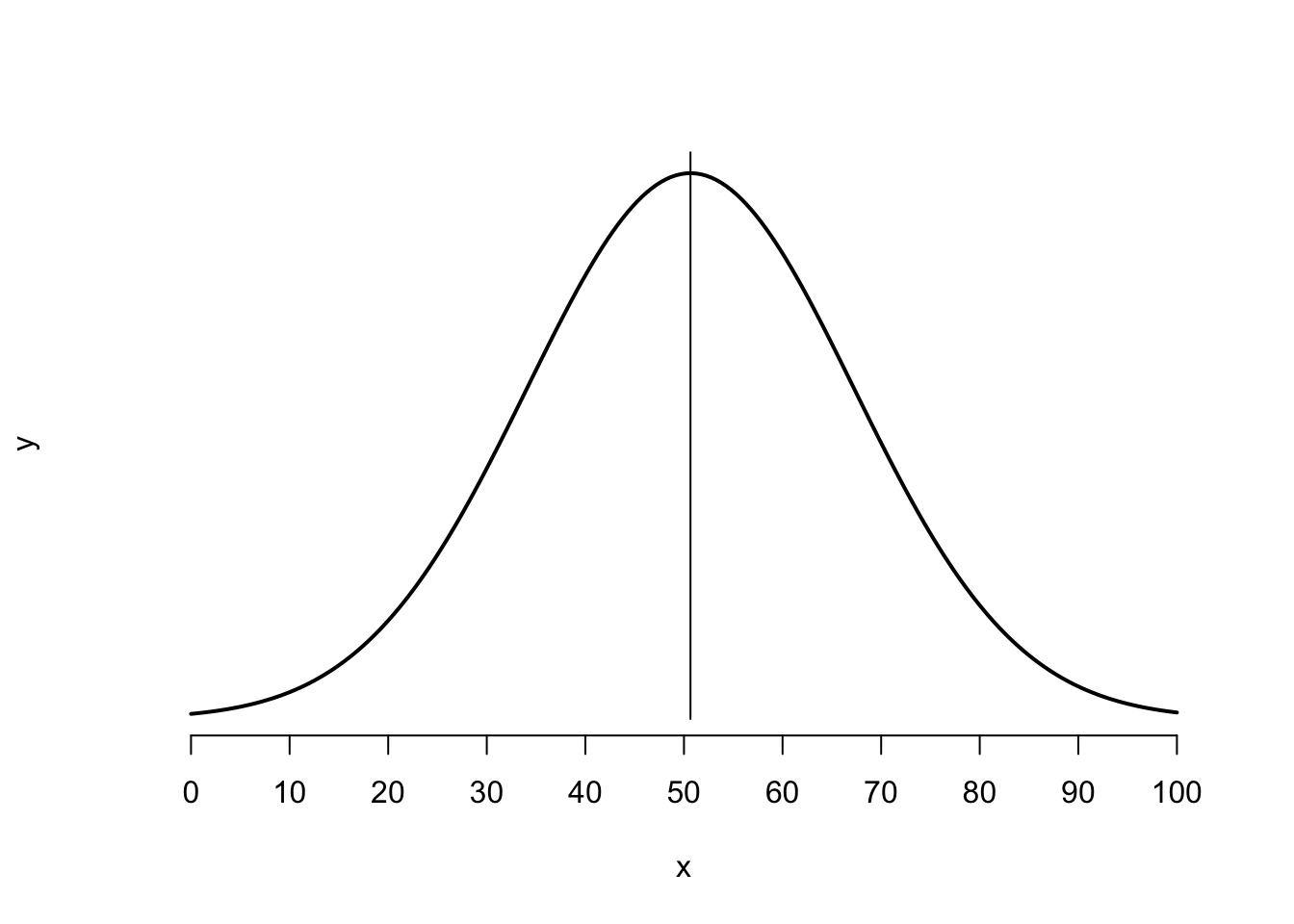
\label{fig:normalmean}Voter Turnout in the 2017 European Elections (n=28)

Figure 7: Voter Turnout in the 2017 European Elections (n=28)

The question then was how likely it was for the EU to achieve a voter turnout larger than the voter turnout in the last General Election in the UK (68.8). If we wanted to visualise this, we would need the area to the right of 68.8 on the x-axis. This would look like this:

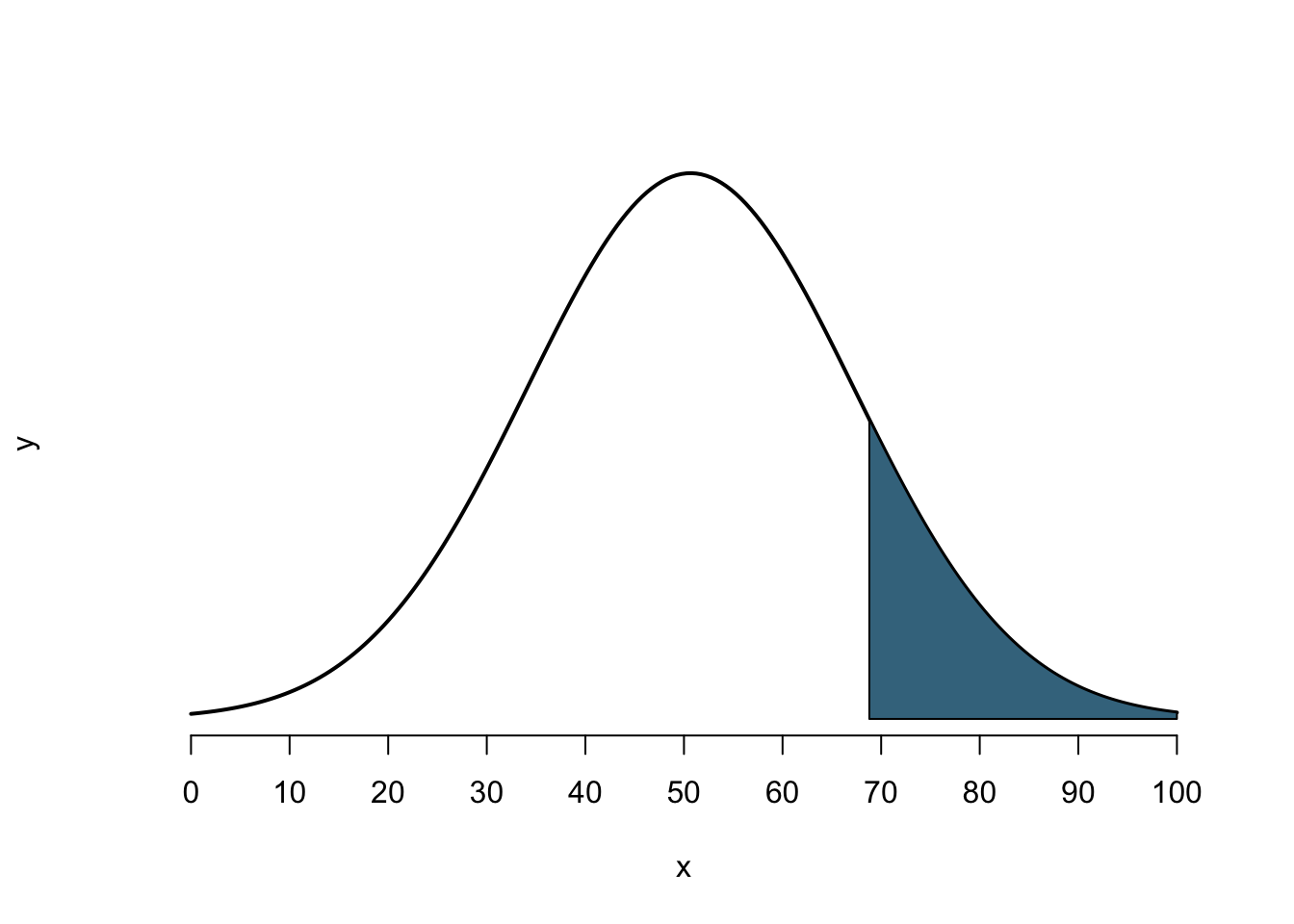
\label{fig:first}Probability of Voter Turnout > 68.8

Figure 8: Probability of Voter Turnout > 68.8

In order to calculate the size of this area, we first took the difference between 68.8 and 50.66 which is 18.14. We then divided 18.14 by the standard deviation of 16.56, to express the distance in units of the standard deviation. The result is 1.095411. We know, therefore, that the point of 68.8 percent voter turnout on the x-axis is located 1.095411 standard deviations to the right of the mean.

We now need to find the right-tail probability that belongs to this value. In the left-most column of the Normal Table you find the z-values with the first decimal place. Move down to 1.1. From here you turn right, until you hit the second decimal place. As our value is 1.10 you will only have to go one column to the right. If the value was 1.11, you would have to go two columns to the right. For a z-score of 1.1 the area is 0.1357, or 13.57%. We can therefore say that with a voter turnout of 50.66 and a standard deviation of 16.56, the probability of achieving a voter turnout higher than 68.6 is 13.57%.

Before moving on, I need to note that z can be negative. If we were assessing the probability of achieving a voter turnout of less than 32.52% (50.66-18.14), we would get a z-score of -1.1. Because the Normal Distribution is symmetrical, we can use the same process, but need to reverse the logic. Because the right tail probability gives us the area to the right of the z-score, a negative z-score would give us the area to the left of the z-score. So the probability of a voter turnout smaller than 32.52 is also 13.57%.

With this knowledge at hand, let’s do some calculations.

Calculations10

  1. The mean weight of a bag of apples is 1 kg. The weight of bags is normally distributed around this mean with a standard deviation of 50g.
    1. Billy is looking for the heaviest bag possible and finds one that is 1082 g. What is the probability of finding a heavier bag?
    2. What is the probability that Billy will find a bag lighter than 870g?
    3. How would the results of a. and b. change if the standard deviation was only 40g? Why?

Solutions

You can find the Solutions in the Downloads Section.

  1. Some of the content of this worksheet is taken from Reiche (forthcoming).↩︎

  2. These are taken from Reiche (forthcoming).↩︎