Confidence Intervals

Self-Assessment Questions11

  1. How do we interpret a confidence interval?
  2. What does the central limit theorem postulate?
  3. Why do we need it?
  4. Why do we need a t-distribution?
  5. What is the difference between the normal distribution and the t-distribution?

Please stop here and don’t go beyond this point until we have compared notes on your answers.

Calculating Confidence Intervals

Just as a reminder, what is a confidence interval?

Confidence Interval

A confidence Interval for a parameter is an interval of numbers within which the parameter is believed to fall. The probability that this method produces an interval that contains the parameter is called the confidence level. This is a number chosen to be close to 1, such as 0.95 or 0.99. (Agresti, 2018, p. 110)

There are two scenarios under which we are calculating confidence intervals: (1) we know \(\sigma\) (the standard deviation of the population distribution), and (2) we don’t know \(\sigma\). Let me take you through these two scenarios in turn:

1. We know \(\sigma\)

If we know the population distribution, then we can use z. Assume we have sample data on the age of students in the university with n=81, and \(\bar{y}=26\). The standard deviation of the population (\(\sigma\)) is 9. We now want an interval within which we find with 99% certainty the true average age of students (we did this example with 95% in the lecture).

We start with calculating the standard error:

\[\begin{equation*} \sigma_{\bar{y}} = \frac{\sigma}{\sqrt{n}} \end{equation*}\]

\[\begin{equation*} \sigma_{\bar{y}} = \frac{9}{\sqrt{81}} = 1 \end{equation*}\]

What is important to bear in mind for the construction of confidence intervals, is that we do not just need the right-tail probability, because the area we are trying to cover under the distribution is symmetrical around the mean. This is visualised in Figure 9 where the area is defined between \(\pm\) 1.96 standard deviations around the mean.

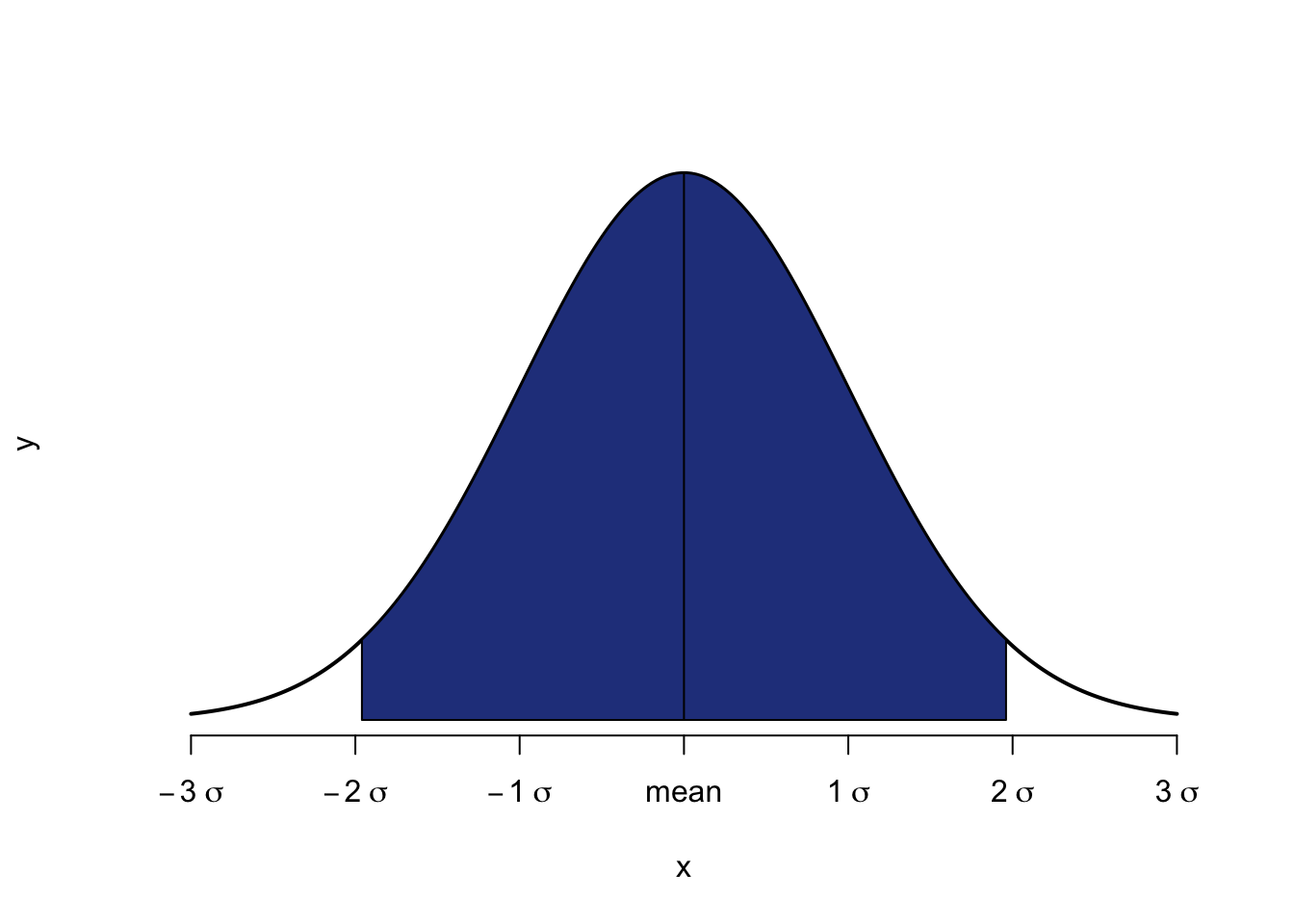
\label{fig:95}95 Percent Confidence Interval around the Mean

Figure 9: 95 Percent Confidence Interval around the Mean

As the grey area needs to be 95%, the white areas to the left and right need to be equal to 5% jointly. So each of them is 2.5%. When we look into our Table with right-tail probabilities, we therefore need to look for the z-score that corresponds to 0.025 (or 2.5%). When you look in the Normal Table (see Statistical Tables), then you will find this at z=1.96.

Now, the question arises, how many standard deviations we need for a 99% confidence interval. The area to the left and right needs to be jointly 1%, or 0.05% each side. We consult the Normal Table again, and try to find the z-score for 0.005. The exact value is not available, only either 0.0051, or 0.0049. 0.0051 would lead to a confidence interval of 98.98%, so not quite large enough. We therefore need to go for 0.0049, and the corresponding z-score of z=2.58.

\[\begin{equation*} \bar{y} \pm 2.58 \times \sigma_{\bar{Y}} \end{equation*}\]

Popping the values in we receive

\[\begin{equation*} 26 \pm 2.58 \times 1 \end{equation*}\]

As a result, we can say that with 99% certainty the true average age of students at Warwick lies between 23.42 and 28.58. Note that this confidence interval is wider than the 95% one where the boundaries were defined as 24.04 and 27.96. As we went for higher certainty here, the confidence interval became wider. If we want our interval to contain the true average in 99 out of 100 samples, we need to cast our net wider than if we were content with 95.

2. We don’t know \(\sigma\)

If we don’t know the population distribution and its standard deviation, we need to use the t-distribution. As you know from the lecture, the t-distribution is a shape shifter. Its width depends on the degrees of freedom: the more degrees of freedom we have, the more narrow, or the closer to the normal distribution it comes. With df=30 the shapes of the t-distribution and the normal distribution are almost identical. You can see this in the following Figure, comparing the yellow t-distribution for \(df=30\) and the black (normal) distribution.

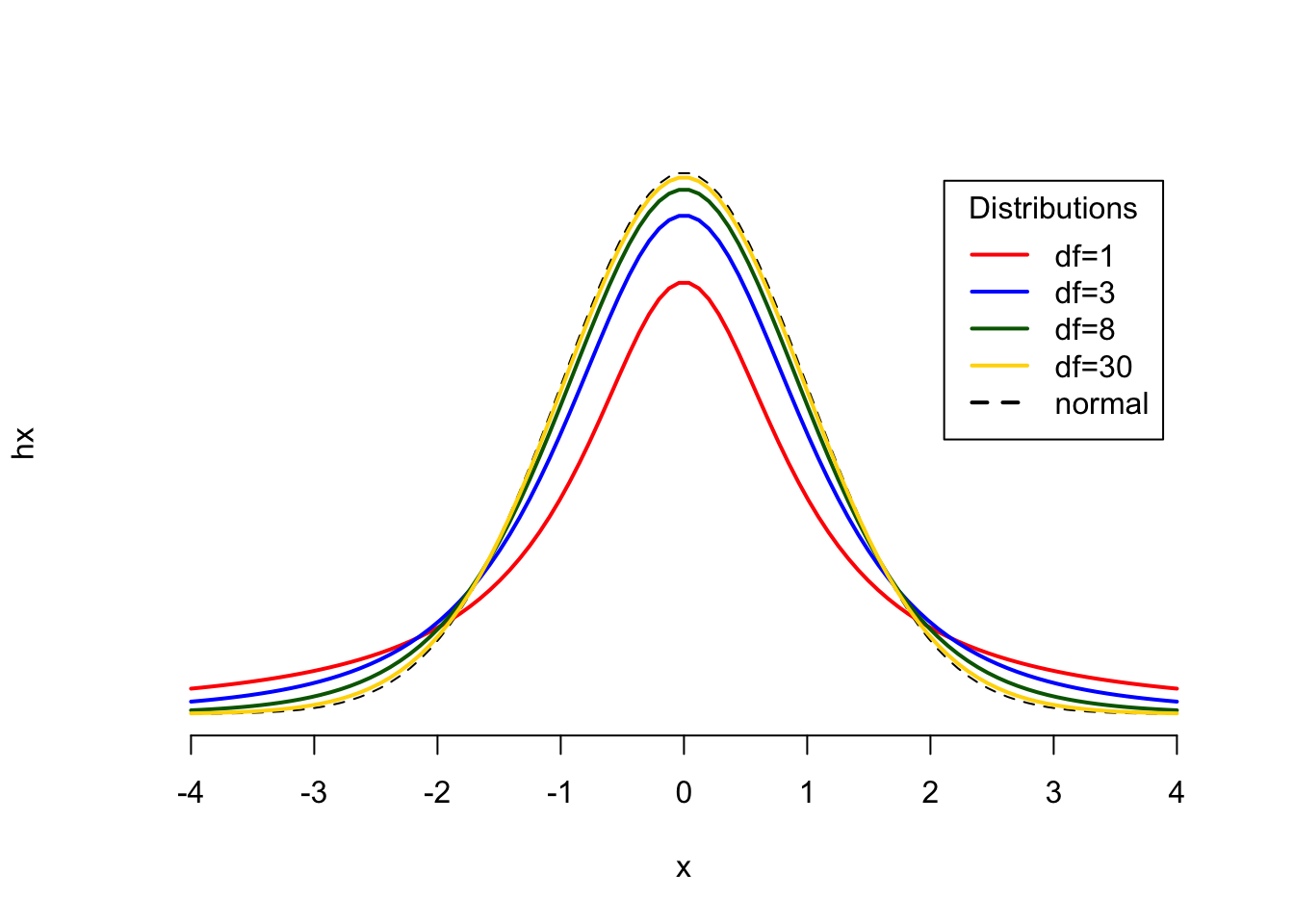
\label{fig:tdistribution}Comparison of t-Distributions

Figure 10: Comparison of t-Distributions

In reversed logic, this also means that the t-distribution is rather wide for small sample sizes (and small df). Consequently, a confidence interval of a given level (e.g. 99%) would be much wider for a small sample size than under the normal distribution (or t-distributions with higher sample sizes). Let me illustrate this using the same sample average as for the normal distribution example above, \(\bar{y}=26\). We have a sample standard deviation (\(s\)) of 2. Our sample size is very small, we only have \(n=4\). Again, we want an interval within which we find with 99% certainty the true average age of students.

We start by estimating the standard error:

\[\begin{equation*} se=\frac{s}{\sqrt{n}} \end{equation*}\]

\[\begin{equation*} se=\frac{2}{\sqrt{4}}=1 \end{equation*}\]

This time we have to search in the t-Table, taking into account the degrees of freedom. As \(n=4\), this means that \(df=3\). Conveniently, the Table lists at the top the desired confidence interval. For \(df=3\) and a 99% confidence interval, the corresponding t-value is 5.841. Once again, we calculate:

\[\begin{equation*} \bar{y} \pm 5.841 \times se \end{equation*}\]

and

\[\begin{equation*} 26 \pm 5.841 \times 1 \end{equation*}\]

The resulting boundaries are 20.159 as the lower boundary, and 31.841 as the upper boundary. This is far wider than the 99% confidence interval we had for the normal distribution, where the lower and upper boundaries were 23.42 and 28.58, respectively. This is a reflection of the fact that we only had a very small sample (\(n=4\)) to base our inference on and therefore have a lot of uncertainty in our inference.

To conclude, it is fair to say that the procedure is essentially the same as with the normal procedure, only that have to go the extra step of taking into account the degrees of freedom.

You are now ready to do some exercises.

Exercises

Conceptual Exercises12

  1. The number of diners visiting a restaurant on a Thursday is normally distributed with a mean of 150 and standard deviation of 30. One Thursday only 100 people eat in the restaurant, and the manager says, “next week will be better”.
    1. What is the probability she is right?
    2. The number of diners on a Friday is also normally distributed with a mean of 200 and a standard deviation of 50. Which two values, symmetrical around the mean contain the number of Friday diners 80% of the time?
  2. A researcher is analysing individuals’ relative fear of being a victim of burglary on a 1-100 scale. This variable is normally distributed. A random sample of 9 individuals found a mean score of 47 on the scale with a sample variance of 158.76 for fear of being burgled.
    1. What distribution would be used to calculate an 80% confidence interval around this mean?
    2. Construct that interval.
    3. Is this a suitable sample size for seeing whether individuals are more nervous around burglary or murder, which is found to have an 80% confidence interval between 2.76 and 14.65?
  3. We are investigating the height of men in the UK. For this we have obtained a random sample of 100 UK men and found they had a mean height of 180cm with a standard deviation of 10cm.
    1. Construct a 95% confidence interval for the mean height of UK males.
    2. Select all true statements concerning the constructed confidence interval and justify your choice for each statement.
      1. The probability of the population mean being within the upper and lower bounds is 95%.
      2. 95% of men’s heights fall between the upper and lower bound.
      3. 95% of the cases in the sample fall between the upper and lower bound.
      4. On average 95% of confidence intervals constructed would contain the population mean.
      5. On average 95% of the means of samples with 100 respondents will fall within the upper and lower bands.
      6. On average 95% of the sample means equal the population mean.

R Exercises

Introduction

For the purpose of this worksheet you will be using a replication data set from Dorff (2011) which provides replication data for the famous study of the determinants of civil war by Fearon & Laitin (2003). This is the abstract, taken from the article:

An influential conventional wisdom holds that civil wars proliferated rapidly with the end of the Cold War and that the root cause of many or most of these has been ethnic and religious antagonisms. We show that the current prevalence of internal war is mainly the result of a steady accumulation of protracted conflicts since the 1950s and 1960s rather than a sudden change associated with a new, post-Cold War international system. We also find that after controlling for per capita income, more ethnically or religiously diverse countries have been no more likely to experience significant civil violence in this period. We argue for understanding civil war in this period in terms of insurgency or rural guerrilla warfare, a particular form of military practice that can be harnessed to diverse political agendas. The factors that explain which countries have been at risk for civil war are not their ethnic or religious characteristics but rather the conditions that favor insurgency. These include poverty – which marks financially and bureaucratically weak states and also favors rebel recruitment – political instability, rough terrain, and large populations.

The fearon dataset contains several variables for each country in 1994, whilst the fearonfull data set contains data for all years from 1945 to 1999. Not all of the operations in the exercises were covered by the material in the lectures / seminars on PO11Q. Some of these rely on the reading, and for some you need to google for help on stackoverflow. You can find a full codebook in Table 3.

Table 3: Codebook to Fearon Data Sets
Variable Label
year 1945-1999
war 0 (no); 1 (yes)
ef ethnic fractionalisation (%)
relfrac religious fractionalisation (%)
pop population (in 1000s)
mtnest mountainous terrain (%)
elevdiff elevation difference of the highest and lowest points (metres)
polity2 regime score: -10 (autocracy) to 10 (democracy)
gdpen GDP per capita (in 1000s, 1985 US Dollar)
Oil less than 1/3 export revenue from oil (0); 1/3 or more export revenue from oil (1)
plural share of largest ethnic group (%)

Exercises

These exercises are deliberately slightly more advanced than those of previous weeks to push you a little. For some of these you will have to use google, as we have not covered all the necessary functions on the module, yet.

  1. Produce a new data frame of df1, df2, df3, df4. For each dataset, arrange them according to countries with:

    1. Lowest Ethnic Fractionalisation
    2. Highest Population
    3. Highest mountainous terrain
    4. Lowest elevation

  2. Create a data frame which looks upon countries that used to be British colonies. Transform the British colony variable into a binary factor of “No” and “Yes”.

  3. Make a dummy variable which shows whether or not a country is majority Muslim, given that the requirement of a majority Muslim country is more than 50% of its population. Do not forget to order the factors.

    1. Use cut()
    2. Use ifelse()

  4. The Polity IV score measures democracy on a scale from -10 to +10 where -10 is equal to perfect autocracy and +10 equal to perfect democracy. Often, the democratisation literature distinguishes between autocracies, anocracies and democracies. We can achieve this differentiation in the Polity IV score as follows:

    • Autocracies: -10 to -6
    • Anocracies: -5 to +5
    • Democracies: +6 to +10

    Using this categorization of polity score; transform the numerical values of polity scores as follows:

    1. Into an ordered factor
    2. Into a binary dummy variable of Democracy/Non-Democracy where only the level “Democracy” of the previous step remains as “Democracy”.

  5. Find the mean difference between:

    1. the share of largest ethnic group and second largest ethnic group.
    2. the share of largest ethnic group and second largest ethnic group within former British colonies (using previous exercise no. 4).

  6. Let’s do some more recoding:

    1. Create an age-group dataframe with the following categories:
    • NA
    • 0-18
    • 18-35
    • 35-50
    • 50-70
    1. Transform the values into numeric values, and separate into a lower and upper category
    2. Create a column - Find the mid of each levels
    3. Create a column - Find the interval of each levels

  7. For this exercise use the data frame fearonfull which contains data for all years between 1945 and 1999. Population is defined in terms of 1,000s.

    1. Create a new data which consists of countries with more than 10000000 people. (large population)
    2. Find the average of population of each large population country from 1945-1999. Hint: group according to country, then find the mean.

  8. Sub-setting data, using the fearonfull data frame:

    1. Extract the necessary variables to compare the social fractionalization between countries.
    2. Retain the last row of the dataset.
    3. Filter the dataset with only countries in an ongoing war (variable ended).
    4. Find the country with an ongoing war in 1999.

  9. Generate a dataframe and find all countries with GDP per capita greater than the world’s mean in 1999 (Function hint: filter)

  10. Generate a dataframe that only consist of data from 1998 and 1999. Change the data format into a wide data using spread for the observations of GDP per capita (you need to use fearonfull again).

  11. Generate a data frame consisting of list of countries and their populations in 1945 and 1995. Find the mean of population differences between 1945 and 1995. Find the mean of population differences between 1945 and 1995 (you need to use fearonfull again).

  12. Calculate the average GDP per capita each oil-producing country has had between 1945 and 1999. Which has the highest mean of GDP per capita (you need to use fearonfull again)?

  13. For this exercise use the fearonfull data set.

    1. Check how many missing values are in the dataset as a whole and in the polity2 variable.
    2. Omit rows with missing values in GDP per capita and population using the filter function.

  14. Use the data in exercise number 13.

    1. Calculate the averages of GDP per capita and population per country between 1945 and 1999. Find the mean GDP per country.
    2. Filter the top 10 highest GDP countries

  15. Find the difference between each country’s largest ethnic group and second largest ethnic group. Arrange the countries in ascending order based on the difference

Homework for Week 9

  • Read the essential literature for the lecture. There is no separate reading for the seminar.
  • Work through this week’s flashcards to familiarise yourself with the relevant R functions.
  • Find an example for each NEW function and apply it in R to ensure it works
  • Work on this week’s R exercises. There are plenty to give you the opportunity to practice with R and I am not expecting you to finish all of them by next week. I recommend doing the first six.

Solutions

You can find the Solutions in the Downloads Section. Please note that the conceptual exercises have a document in the “Documents” Section, whereas the solutions to the R Exercises are in an RScript in the section of the same name.

  1. Some of the content of this worksheet is taken from Reiche (forthcoming).↩︎

  2. These are taken from Reiche (forthcoming).↩︎